문 제

소 스 코 드
// 벨만 - 포드 알고리즘
#include <iostream>
#include <vector>
#include <algorithm>
constexpr int INF{ 0x7fff'0000 };
struct Edge {
int nVector;
int mWeight;
};
class Graph {
public:
Graph() = delete;
Graph(const int v) {
mGraph.resize(v + 1);
mDist.resize(v + 1);
}
void AddEdge(const int& a, const int b, const int c) {
mGraph[a].emplace_back(Edge{ b, c });
// mGraph[b].emplace_back(Edge{ a, c });
}
bool cycle{ false };
void BellmanFord(const int& start) {
for (int i = 1; i < mDist.size(); ++i) mDist[i] = INF;
mDist[start] = 0;
for (int k = 1; k < mGraph.size(); ++k) {
for (int i = 1; i < mGraph.size(); ++i) {
if (INF == mDist[i]) continue;
for (int j = 0; j < mGraph[i].size(); ++j) {
int next{ mGraph[i][j].nVector };
int weight{ mGraph[i][j].mWeight };
if (mDist[next] > mDist[i] + weight) {
mDist[next] = mDist[i] + weight;
if (k == mGraph.size() - 1) cycle = true;
}
}
}
}
if (cycle) std::cout << "-1 \n";
else {
for (int i = 2; i < mDist.size(); ++i) {
if (INF != mDist[i]) std::cout << mDist[i] << "\n";
else std::cout << "-1 \n";
}
}
}
private:
std::vector<std::vector<Edge>> mGraph;
std::vector<long long> mDist;
};
int main() {
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
std::cout.tie(NULL);
int N, M;
std::cin >> N >> M;
Graph graph(N);
int A, B, C;
for (int i = 0; i < M; ++i) {
std::cin >> A >> B >> C;
graph.AddEdge(A, B, C);
}
graph.BellmanFord(1);
return 0;
}
풀 이
-
벨만-포드 알고리즘 ( Bellman-Ford's Algorithm )
더보기
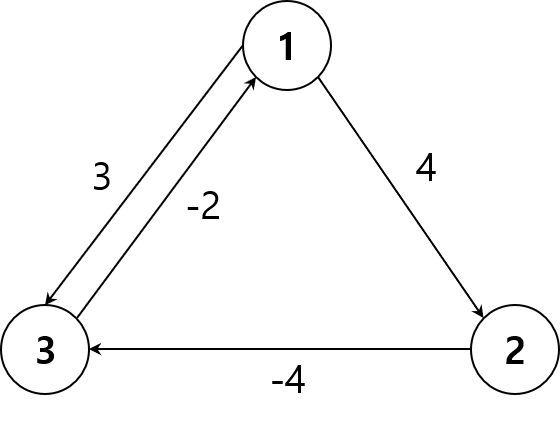
다익스트라 알고리즘과, 벨만-포드 알고리즘의 차이가 무엇인가?
제가 생각하기에는 다익스트라 알고리즘의 특정한 추가 코드 없이 실행 시킨다면,
만약, 점과 점을 잇는 선의 무게가 -가 될 경우,
무한으로 값이 작아지기 때문에, 이 무한으로 작아지는 부분을 파악하여 조건을 넣지 않으면
올바르게 작동하지 않는다.
벨만-포트 알고리즘의 경우,
모든 점에 대하여, $$D(a, b) = D(a, u) + W(u,b)$$
a부터 b까지의 최단 경로는 a부터 u까지의 누적 거리와 u에서 b까지의 선의 무게를 더한 값이다.

위의 이미지와 같은 그래프를 가질 경우,
계속, 순환하여 - ∞ 로 가기 때문에, -1의 결과 값을 찾을 수 있다.
이 때, -의 값이 int의 값을 넘어갈 수 있기 때문에, long long으로 저장해야 한다.
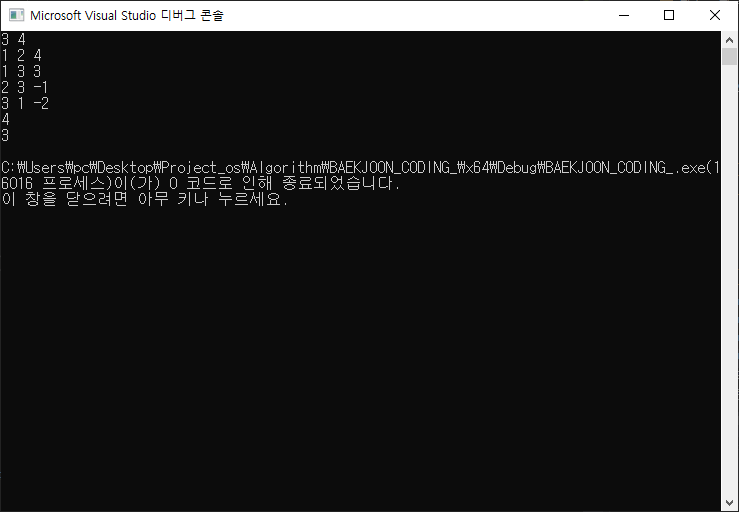
출 력 값
문 제 출 처
문제 링크 : www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
'[ ALGORITHM ] > [ 백 준 ]' 카테고리의 다른 글
| [BAEKJOON] 10217번 : KCM Travel* (0) | 2020.09.15 |
|---|---|
| [BAEKJOON] 11404번 : 플로이드 (0) | 2020.09.11 |
| [BAEKJOON] 9370번 : 미확인 도착지 (0) | 2020.09.09 |
| [BAEKJOON] 1504번 : 특정한 최단 경로 (0) | 2020.09.08 |
| [BAEKJOON] 1753번 : 최단경로 (0) | 2020.09.07 |